Max Subarray in Haskell by David Lettier

The Problem

We have a list or array of integers and wish to know what is the maximum positive sum we can find contained in some subarray in the list.

So for example say our array was [-1,2,3,4] then all the subarrays would be:

[-1] [2] [3] [4]
[-1,2] [2,3] [3,4]
[-1,2,3] [2,3,4]
[-1,2,3,4]

and the max subarray would be [2,3,4] for a total of 9. So subarray is defined as some section or the entire collection of the contiguous elements found in the array. For example [-1,4,3] would not be a subarray.

The problem was first posed by Ulf Grenander of Brown University in 1977, as a simplified model for maximum likelihood estimation of patterns in digitized images. A linear time algorithm was found soon afterwards by Jay Kadane of Carnegie-Mellon University (Bentley 1984).
Maximum subarray problem, Wikipedia

We’ll also throw in a twist and say that if our array has only negative integers then we want the maximum one. And as an added kicker we will want to know what is the largest positive sum of any collection of elements in the array.

The Solution

One way to solve this problem would be to keep track of two indexes i and j and iterate through the array from 0 to N-1 for i and for each one of those iterations iterate through the array again from i to N-1 for j. Each time you iterate you take a slice of the array, compute the sum, and take the max of the sum and what you have seen already.

-- Puesdo code

{-
  max_sum = 0
  a = [...]
  N = length(a)
  for i in 0 through N-1
    for j in i through N-1
      max_sum = max(max_sum, sum(a[i through j])
  return max_sum

  For a=[-1,2,3,4] this works out to:

  max_sum = 0
  max_sum = max(max_sum, sum([-1]))        -
  max_sum = max(max_sum, sum([-1,2]))      |
  max_sum = max(max_sum, sum([-1,2,3]))    |
  max_sum = max(max_sum, sum([-1,2,3,4]))  |
  max_sum = max(max_sum, sum([2]))         -
  max_sum = max(max_sum, sum([2,3]))       |
  max_sum = max(max_sum, sum([2,3,4]))     |
  max_sum = max(max_sum, sum([3]))         -
  max_sum = max(max_sum, sum([3,4]))       |
  max_sum = max(max_sum, sum([4]))         -
-}

For the first inner iteration we do four steps and then afterward we do three, then two, and then one step for a total of 10 steps. If the array was size five we would have done five, four, three, two, and then one step for a total of 15 steps. This works out to n(n+1)/2 steps for an array of size n (triangle numbers). So the number of steps of this algorithm is roughly n^2 (excluding the steps needed to sum each subarray).

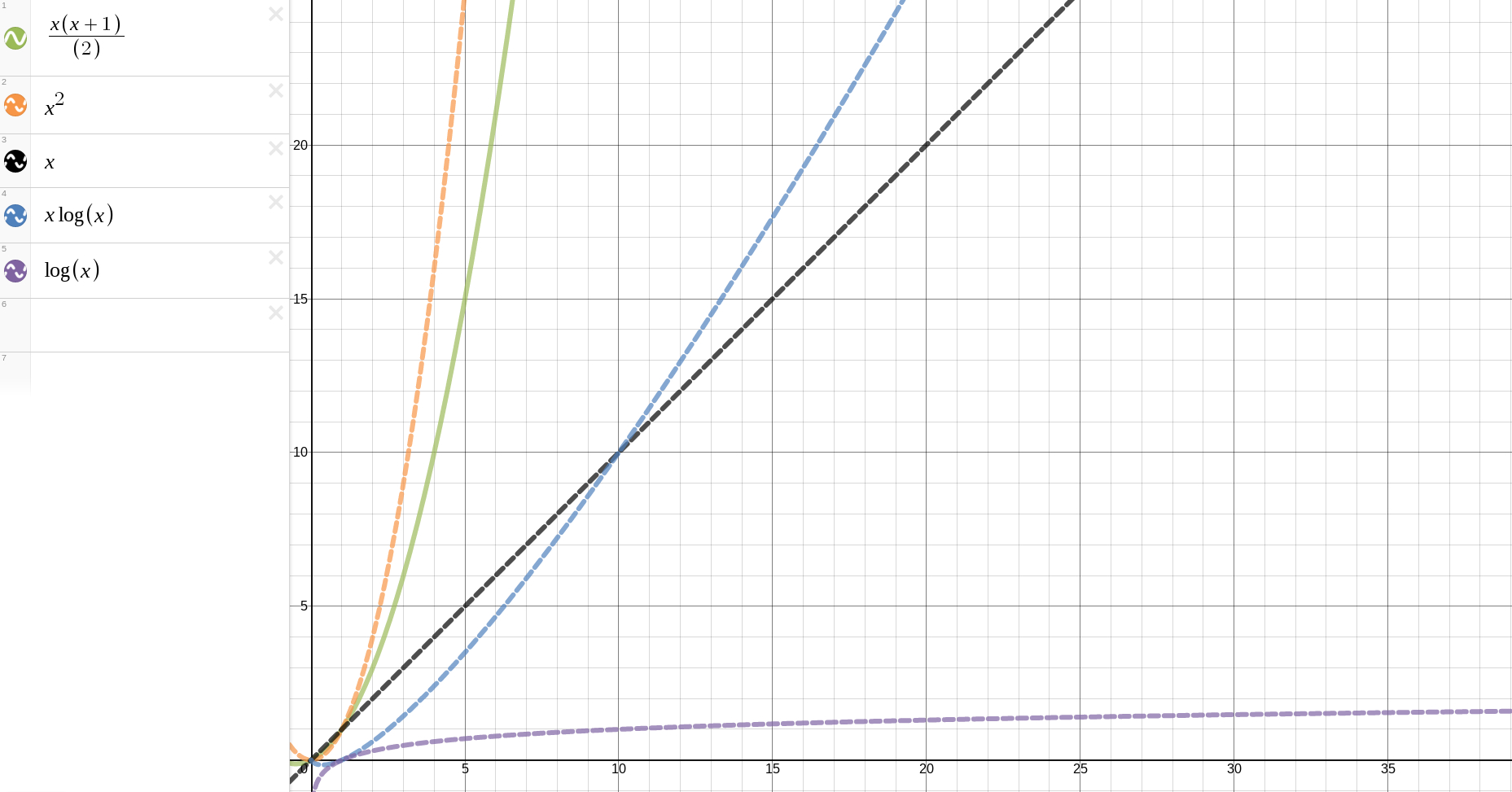
Run Time Comparisons

Another way would be to enumerate through all of the possible subarrays summing each one and keeping track of the largest one. First you would sum all of the subarrays of size one and remember the largest. Then you would sum all of the subarrays of size two and so on and so fourth until you summed the entire array. However this is more or less the same as the previous approach. Both of these approaches preform redundant work. If you checked [2,3] then you do not have to check [2,3,4] from scratch.

The approach we will take is a linear time algorithm known as Kadane's algorithm. If you have never read Haskell before, do not worry as it will be straight forward.

We will begin by looking at our input.

Number of arrays
First array number of items
First array items
Second array number of items
Second array items
.
.
.
Nth array number of items
Nth array items

N
3
1 -2 3
4
1 2 -3 4
.
.
.
10
1 -2 3 4 -5 6 -7 8 9 10

So we will need to process each line and gather up all of the arrays.

1) main :: IO ()
2) main = do
3)   input <- fmap ((map words) . lines) getContents
4)   let arrays = map snd $ filter (\(x, y) -> (mod x 2) /= 0) $ zip [0..] (tail input)
5)   let arrays' = map (\x -> map (\y -> read y :: Int) x) arrays
6)   mapM_ (\ x -> putStrLn (max_cont_ncont_sum x)) arrays'

Line one is just defining our main function much like in C. Line three says hey get the entire input, break it up into an array of lines, for each line split the line into words, and then store this in input. Line four and five are pulling out the actual arrays in the input. First we will discard, by calling (tail input), the first input line which says how many arrays there are. This is what we mean by tail or put another way: everything but the head or first part.

Starting at zero (after removing the head), each array is at one, three, five, etc. So we know that each array is at in odd position in the input. Note that /= means not equal !=. Of course all of this input is in string form so we run through each array found and turn each array element into an integer. Line five is where the magic happens and we’ll get to that shortly.

1) max_cont_ncont_sum :: [Int] -> String
2) max_cont_ncont_sum array = (show a)  ++ " " ++ (show b)
3)   where  cont = max_cont_sum array 0 0
4)          ncont = max_ncont_sum array
5)          max_elem = maximum array
6)          a = if cont == 0 then max_elem else cont
7)          b = if ncont == 0 then max_elem else ncont

Line one is defining this helper function we need to show both the max subarray sum and the max sum of non-contiguous elements. It takes a list of integers and then builds a string as output. The where clauses, starting on line three, build up the variables a and b. cont is the output of max_cont_sum which is the sum of the max subarray. ncont is the output of max_ncont_sum which is the maximum sum of the non-contiguous elements in the array.

Recall that we wanted the largest negative integer if all of the integers in the array were negative. So for lines four through six we set a and/or b to be max_elem if either cont and/or ncont are zero, else a equals cont and b equals ncont. Both cont and ncont will be zero if all elements in the array are negative so both a and b will be equal to max_elem (maximum element).

Now we get to the meat but we will start with the easier function max_ncont_sum.

max_ncont_sum :: [Int] -> Int
max_ncont_sum = foldl (\acc x -> if x >= 0 then acc + x else acc + 0) 0

foldl stands for reduce this array starting from the left. The last zero at the end of the line is the first element we will fold and will be the first to show up in acc (the accumulator). You’ll notice that it looks like max_ncont_sum does not take any arguments or parameters but it does. foldl take three parameters: a function, a starting value, and an array. max_ncont_sum has one parameter and it too expects an array. max_ncont_sum in this form is partially applying foldl returning a new function that is waiting on being passed an array.

Partial application means taking a function and partially applying it to one or more of its arguments, but not all, creating a new function in the process.
Dave Atchley

The lambda or anonymous function we gave to foldl

(\acc x -> if x >= 0 then acc + x else acc)

takes two parameters and outputs acc + x if x is positive otherwise it just outputs acc. This function is called for every element in the array. The accumulator acc holds the output from the last time our anonymous function was called. If we only ever accumulate or sum up positive numbers you can see how this will find the maximum sum of all of the non-contiguous elements in the array. And if there are no positive elements in the array, the acc will only ever hold that first 0 we passed to foldl.

Prelude> foldl (\acc x -> if x >= 0 then acc + x else acc) 0 [1,2,3,4,-5,2,1,1,1,-1]
15

Now we arrive to the heart of the solution.

1) max_cont_sum :: [Int] -> Int -> Int -> Int
2) max_cont_sum [] _ maxx = maxx
3) max_cont_sum (h:t) sub_max maxx = max_cont_sum t (max 0 sub_max_cur) (max sub_max_cur maxx)
4)   where sub_max_cur = sub_max + h

Line one is the definition of max_cont_sum which takes an array (list of integers), a starting sub_max (integer), a starting maxx (integer), and returns the maxx (an integer). Lines two and three are different cases that determine what happens next. If the array is empty then just return maxx–whatever it may be at the moment. Otherwise have this function call itself with one less array element (lose the head and take the tail), the max between 0 and sub_max_cur (sub max current), and the max between sub_max_cur and maxx. Line four defines sub_max_cur as sub_max, passed to the function, plus the first element in the array (the h in (h:t) short for head).

Let us run through this using [1,-2,3,4,-1,1].

1) max_cont_sum [1,-2,3,4,-1,1] 0 0 = max_cont_sum [-2,3,4,-1,1] 1 1
2)   where sub_max_cur = 0 + 1

1) max_cont_sum [-2,3,4,-1,1] 1 1 = max_cont_sum [3,4,-1,1] 0 1
2)   where sub_max_cur =  1 + -2

1) max_cont_sum [3,4,-1,1] 0 1 = max_cont_sum [4,-1,1] 3 3
2)   where sub_max_cur = 0 + 3

1) max_cont_sum [4,-1,1] 3 3 = max_cont_sum [-1,1] 7 7
2)   where sub_max_cur = 3 + 4

1) max_cont_sum [-1,1] 7 7 = max_cont_sum [1] 6 7
2)   where sub_max_cur = 7 + -1

1) max_cont_sum [1] 6 7 = max_cont_sum [] 7 7
2)   where sub_max_cur = 6 + 1

1) max_cont_sum [] _ 7 = 7

7

All of the subarrays are:

[1] [-2] [3] [4] [-1] [1]
[1,-2] [-2,3] [3,4] [4,-1] [-1,1]
[1,-2,3] [-2,3,4] [3,4,-1] [4,-1,1]
[1,-2,3,4] [-2,3,4,-1] [3,4,-1,1]
[1,-2,3,4,-1] [-2,3,4,-1,1]
[1,-2,3,4,-1,1]

The max subarray is [3,4] giving us a total of 7. The solution is not unique however as [3,4,-1,1] could also be the max subarray. sub_max never goes below 0 and climbs and falls until sub_max_cur goes negative at which point sub_max resets to zero. maxx never goes below its current value and always equals sub_max’s historical peak, that is, the value it climbed highest to so far in the array. You can see that once sub_max reached higher and higher peaks (even after falling back down) maxx kept the max seen so far.

Putting it all together:

-- David Lettier (C) 2016.
-- http://www.lettier.com/

max_cont_sum :: [Int] -> Int -> Int -> Int
max_cont_sum [] _ maxx = maxx
max_cont_sum (h:t) sub_max maxx = max_cont_sum t (max 0 sub_max_cur) (max sub_max_cur maxx)
  where sub_max_cur = sub_max + h

max_ncont_sum :: [Int] -> Int
max_ncont_sum = foldl (\acc x -> if x >= 0 then acc + x else acc + 0) 0

max_cont_ncont_sum :: [Int] -> String
max_cont_ncont_sum array = (show a)  ++ " " ++ (show b)
  where  cont = max_cont_sum array 0 0
         ncont = max_ncont_sum array
         max_elem = maximum array
         a = if cont == 0 then max_elem else cont
         b = if ncont == 0 then max_elem else ncont

main :: IO ()
main = do
  input <- fmap ((map words) . lines) getContents
  let arrays = map snd $ filter (\(x, y) -> (mod x 2) /= 0) $ zip [0..] (tail input)
  let arrays' = map (\ x -> map (\y -> read y :: Int) x) arrays
  mapM_ (\x -> putStrLn (max_cont_ncont_sum x)) arrays'

Recap

We defined the max or maximum subarray problem as finding the maximum sum of some subarray of contiguous values found in the array. On top this, we added an extra stipulation of finding the maximum sum of non-contiguous elements. Before we could begin, we had to parse and convert the input into arrays of integers. For finding the non-contiguous max sum, we used the foldl or reduce function. For the max subarray problem, we employed a recursive solution keeping track of two inputs where the base case was an empty array.

If you enjoy these types of problems be sure to join me on HackerRank.

Max Subarray in Haskell |

The Problem

The Solution

Recap

Hi there! Browse and subscribe to the RSS feed for more content.

2017 David Lettier