Boost your skills, how to easily write K-Means by David Lettier

The final product

You can play with the final build at lettier.com/kmeans. All of its source is stored on GitHub.

K-Means

K-Means is an unsupervised machine learning technique that (hopefully) clusters similar items/data-points given. The entire algorithm consists of the following three major steps.

Initialization
Assignment
Update

K-means clustering aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean, serving as a prototype of the cluster.
K-Means Clustering, Wikipedia

One of the caveats with k-means is that you must know (or guess) the number of clusters k before clustering.

Mean initialization

At the start of the algorithm you must initialize the means’ features/coordinates in the X dimensional space your data points reside in. For example, the features/dimensions for fruit could be:

[circumfrence, height, volume, sugar grams, ...]

We will offer two initialization methods for our k-means object:

Random
The Fouad Khan Method

Other methods include randomly choosing k data points as the starting means and k-means++.

Random

The first method randomly scatters the k means throughout the feature space making sure not to go outside the bounds of the input data points.

KMeans.prototype.initializeMeansMethod0 = function () {
  if (this.means.length == this.k) {
    return;
  }

  this.means.length = 0;

  var k = this.k;
  while (k--) {
    var i = this.featureLength;
    var mean = new Mean();
    mean.id = k;
    while (i--) {
      var min = this.featuresMin[i];
      var max = this.featuresMax[i];
      var value = randomValueInRange(max, min);
      mean.features.unshift(value);
    }
    this.means.push(mean);
  }
};

The Fouad Khan method

The following initialization method is outlined in Fouad Khan’s paper.

KMeans.prototype.initializeMeansMethod1 = function () {
  var mean = null;
  var magnitudeSortedDataPoints = [];
  var consecutiveDataPointDistances = [];
  var sortedConsecutiveDataPointDistances = [];
  var upperBoundIndexes = [];
  var lowerBoundIndexes = [];
  var upperLowerBoundDataPoints = [];
  var i = 0;

We will begin by defining all of our variables upfront at the start of the method.

  this.dataPoints.forEach(function (dataPoint) {
    dataPoint.magnitude = magnitude(dataPoint);
  });

  magnitudeSortedDataPoints = this.dataPoints.sort(
    compareDataPointMagnitudes
  );

  if (magnitudeSortedDataPoints.length === 0) {return;}

  if (magnitudeSortedDataPoints.length === 1) {
      mean = new Mean();
      mean.id = 0;
      mean.features = magnitudeSortedDataPoints[0].features;
      this.means.push(mean);
      return;
  }

The algorithm starts off with finding the magnitude–length of the vector from the origin [0,0] to the data point–of each data point. We then sort these data points by their magnitudes where the first is the closest to the origin and the last is the farthest away.

If we have no data points, just return. If we only have one, just set it as the mean.

  function ConsecutiveDataPointDistance(dataPoint, distance, index) {
    this.dataPoint = dataPoint;
    this.distance = distance;
    this.index = index;
  }

  //...

  for (i=1; i<magnitudeSortedDataPoints.length; ++i) {
    var d1 = magnitudeSortedDataPoints[i];
    var d0 = magnitudeSortedDataPoints[i-1];
    var consecutiveDataPointDistance = new ConsecutiveDataPointDistance(
      d0,
      this.euclideanDistance(d1, d0),
      i-1
    );
    consecutiveDataPointDistances.push(consecutiveDataPointDistance);
  }

  sortedConsecutiveDataPointDistances = consecutiveDataPointDistances.sort(
    compareConsecutiveDataPointDistances
  );

Now we take these data points, sorted by their magnitudes, and compute the euclidean distance between each of them.

d0 <---distance---> d1 <---distance---> d2 <---distance---> ... dn-1

And similarly with the magnitudes, we sort the data points di by the distance to their next neighbor di+1 but in descending order.

So say we have three data points:

d0:
  Magnitude Index: 0
  Magnitude: 1
  Distance to d1: 1
d1:
  Magnitude Index: 1
  Magnitude: 2
  Distance to d2: 2
d2:
  Magnitude Index 2
  Magnitude: 3
  Distance to null: 0

they would be sorted like so:

d1:
  Magnitude Index: 1
  Magnitude: 2
  Distance to d2: 2
d0:
  Magnitude Index: 0
  Magnitude: 1
  Distance to d1: 1
d2:
  Magnitude Index 2
  Magnitude: 3
  Distance to null: 0

Note that we remember the index they had in the magnitudeSortedDataPoints.

  for (i=0; i<(this.k - 1); ++i) {
    upperBoundIndexes.push(
      sortedConsecutiveDataPointDistances[i].index
    );
  }
  upperBoundIndexes.push(magnitudeSortedDataPoints.length - 1);
  upperBoundIndexes = upperBoundIndexes.sort(function (a, b){ return a - b; });

Using the sorted consecutive data points’ distances, we now need to gather the upper and lower cluster bounds. The upper bounds are the first k-1 magnitudeSortedDataPoints indexes in the sortedConsecutiveDataPointDistances plus the last index in magnitudeSortedDataPoints. With the upper bound indexes added, we sort them in ascending order.

  lowerBoundIndexes.push(0);
  for (i=0; i<(upperBoundIndexes.length - 1); ++i) {
    lowerBoundIndexes.push(upperBoundIndexes[i] + 1);
  }

For each upper bound index i, the corresponding lower bound index is i + 1. Index 0 is added at the beginning.

  for (i=0; i<upperBoundIndexes.length; ++i) {
    var temp = [];
    temp.push(
      magnitudeSortedDataPoints[upperBoundIndexes[i]]
    );
    temp.push(
      magnitudeSortedDataPoints[lowerBoundIndexes[i]]
    );
    upperLowerBoundDataPoints.push(temp);
  }

For convenience we’ll create an array of arrays such that each array is [upper index, lower index].

  for (i=0; i<upperLowerBoundDataPoints.length; ++i) {
    mean = new Mean();
    mean.id = i;
    mean.features = this.meanFeatures(
      upperLowerBoundDataPoints[i]
    );
    this.means.push(mean);
  }

We can now compute the mean of the features between each upper and lower bound where each upper and lower bound is one of the input data points. For each pair, the mean of their features become the initial means we will use to cluster all of the data points.

The methodology discussed above simply draws the cluster boundaries at points in the data where the gap between consecutive data values is the highest or the data has deepest “valleys”.
Fouad Khan

To make this initialization method more concrete, imagine we have the following six data points:

"dataPoints":[
  {
    "features":[1,2],
    "magnitude":2.23606797749979,
    "index":0
  },
  {
    "features":[2,3],
    "magnitude":3.605551275463989,
    "index":1
  },
  {
    "features":[3,4],
    "magnitude":5
    "index":2
  },
  {
    "features":[10,11],
    "magnitude":14.866068747318506
    "index":3
  },
  {
    "features":[11,12],
    "magnitude":16.278820596099706
    "index":4
  },
  {
    "features":[12,13],
    "magnitude":17.69180601295413
    "index":5
  }
]

Data points’ Magnitudes

The magnitudes have already been calculated and the data points have been sorted in ascending order by their magnitude. Notice the large gap between the [3,4] and [10,11] magnitudes.

"dataPoints":[
  {
    "features":[3,4],
    "magnitude":5
    "index":2,
    "distanceToNext":9.899495
  },
  {
    "features":[1,2],
    "magnitude":2.23606797749979,
    "index":0,
    "distanceToNext":1.414214
  },
  {
    "features":[2,3],
    "magnitude":3.605551275463989,
    "index":1,
    "distanceToNext":1.414214
  },
  {
    "features":[10,11],
    "magnitude":14.866068747318506
    "index":3,
    "distanceToNext":1.414214
  },
  {
    "features":[11,12],
    "magnitude":16.278820596099706
    "index":4,
    "distanceToNext":1.414214
  },
  {
    "features":[12,13],
    "magnitude":17.69180601295413
    "index":5,
    "distanceToNext":null
  }
]

Data points’ Distances to Next

We compute the distances between each and sort them by their distanceToNext.

Now say our k is two such that we want to cluster these data points into two clusters.

"upperBoundDataPoints":[
  {
    "features":[3,4],
    "magnitude":5
    "index":2,
    "distanceToNext":9.899495
  },
  {
    "features":[12,13],
    "magnitude":17.69180601295413
    "index":5,
    "distanceToNext":null
  }
]

We identify k-1 highest distances, sort by index in ascending order, and add in the last index. Recall that the highest distance-to-next was [3,4] and the last index was 5 for the data point [12,13]. These are our upperBoundDataPoints.

"lowerBoundDataPoints":[
  {
    "features":[1,2],
    "magnitude":2.23606797749979,
    "index":0,
    "distanceToNext":1.414214
  },
  {
    "features":[10,11],
    "magnitude":14.866068747318506
    "index":3,
    "distanceToNext":1.414214
  }
]

The lower bound indexes are the first one (index 0) and then the index + 1 for all upper bound indexes except the last one (in this case index five). So indexes 0 and 2 + 1 = 3. Recall that index 0 was the data point closest to the origin.

"upperLowerBoundDataPoints":[
  [
    {
      "features":[3,4],
      "magnitude":5
      "index":2,
      "distanceToNext":9.899495
    },
    {
      "features":[1,2],
      "magnitude":2.23606797749979,
      "index":0,
      "distanceToNext":1.414214
    }
  ],
  [
    {
      "features":[12,13],
      "magnitude":17.69180601295413
      "index":5,
      "distanceToNext":null
    },
    {
      "features":[10,11],
      "magnitude":14.866068747318506
      "index":3,
      "distanceToNext":1.414214
    }
  ]
]

Now we couple the upper with its lower bound counterpart.

Upper and Lower Bounds

"means":[
  {
    "features":[2,3],
    "id":0
  },
  {
    "features":[11,12],
    "id":1
  }
]

We compute the means between each feature index and create our new initial means.

mean 0:
  [(3 + 1)/2, (4 + 2)/2]
meant 1:
  [(12 + 10)/2, (13 + 11)/2]

Note that the means in this case happen to correspond to the two data points:

"dataPoints":[
  {
    "features":[2,3],
    "magnitude":3.605551275463989,
    "index":1,
    "distanceToNext":1.414214
  },
  {
    "features":[11,12],
    "magnitude":16.278820596099706
    "index":4,
    "distanceToNext":1.414214
  }
]

which are the two points across the large cap and in between their closest neighbors.

Initialized Means

Assignment

With our means initialized, we can begin assigning them to each data point.

KMeans.prototype.assignmentStep = function () {
  for (var i=0; i<this.dataPoints.length; ++i) {
    var dataPoint = this.dataPoints[i];
    var euclideanDistances = [];
    for (var j=0; j<this.means.length; ++j) {
      var mean = this.means[j];
      euclideanDistances.push(
          {
            euclideanDistance: this.euclideanDistance(
              dataPoint,
              mean
            ),
            meanId: mean.id
          }
      );
    }
    this.dataPoints[i].meanId = euclideanDistances.sort(
      this.compareEuclideanDistances
    )[0].meanId;
  }
};

Each data point is assigned to its closest mean based on the euclidean distance from it to the mean. We keep track of the assignment by setting the mean ID on the data point object. Each mean has a unique identifier.

Update

With every data point assigned to a mean, we can now update each mean’s features based on the data points assigned to each one.

KMeans.prototype.updateStep = function () {
  var newMeans = [];
  var clusters = [];
  var k = this.k;
  var converged = 0;
  var that = this;

  while (k--) {
    clusters.push([]);
  }

  for (i=0; i<this.dataPoints.length; ++i) {
    dataPoint = this.dataPoints[i];
    clusters[dataPoint.meanId].push(dataPoint);
  }

  this.clusters = clusters;
  this.converged = false;

  for (i=0; i<this.means.length; ++i) {
    var equal = 0;
    var newMeanFeatures = this.meanFeatures(
      clusters[this.means[i].id]
    );

    for (var j=0; j<this.featureLength; ++j) {
      if (newMeanFeatures[j] === this.means[i].features[j]) {
        equal +=1;
      }
    }

    if (equal === this.featureLength) {converged += 1;}

    this.means[i].features = newMeanFeatures;
  }

  if (converged === this.k) {this.converged = true;}
};

First we reset the clusters and then cluster each data point based on its mean ID. With the clusters populated, we compute the mean of all the features of all the data points per cluster. For each cluster, these averaged features become the new features/coordinates of the mean. Each time this is called, the means will move across the dimensional space until the updates no longer change. When no changes occur we can say the algorithm converged.

Iterate

KMeans.prototype.iterate = function () {
  var iterations = 0;
  var that = this;

  if (this.dataPoints.length === 0) {return;}

  this.featureBounds();
  this.initializeMeans(1);

  var cycle = function () {
    if (that.dataPoints.length === 0) {return;}

    if (iterations <= that.maxIterations && that.converged === false) {
      that.assignmentStep();
      that.updateStep();
      that.onIterate(that);
      iterations += 1;
      window.requestAnimationFrame(cycle);
    } else {
      that.onComplete(that);
      return;
    }
  };
  window.requestAnimationFrame(cycle);
};

Each iteration involves one assignment step and one update step. Remember that each assignment step assigns each data point to its closest mean and that each update steps moves the mean based on the average features of all the data points in its cluster.

So that we do not hang the browser while k-means runs, we perform the iterations by queuing requested animation frames. This allows the application to still be responsive while we progress towards convergence (or max iterations, whichever comes first). While we are not explicitly doing any actual animation each call, the onIterate function callback is called. When the KMeans object is used in canvas.js, the onIterate callback does update the visual means’ positions and the dots’ cluster membership colors. This allows the user to see k-means progress instead of just seeing the final result after the stop criteria is met. Another approach would be to use setTimeout.

Silhouette Coefficient Metric

Even though k-means is unsupervised we can still check its solution using the silhouette coefficient metric. Not all cluster configurations produced by k-means will be the most optimal or even remotely correct. This is especially the case when the wrong k is chosen.

The silhouette coefficient for a single data point is s = (b - a) / max(b, a) where a is the mean distance between a data point and its cluster members and b is the mean distance between a data point and the cluster members of the nearest cluster closest to the data point’s cluster.

Constructor

function SilhouetteCoefficient(params) {
  this.dataPointClusterMembersFunction = params.dataPointClusterMembersFunction;
  this.dataPointNearestClusterMembersFunction = params.dataPointNearestClusterMembersFunction;
  this.distanceFunction = params.distanceFunction;
}

The constructor requires three functions:

One to return the cluster members for a data point
One to return the cluster members of the nearest cluster to the cluster a data point is assigned to
One to calculate the distance

The formula

Recall that the formula for the Silhouette Coefficient is s = (b - a) / max(b, a).

A

SilhouetteCoefficient.prototype.a = function (dataPoint) {
  var dataPointClusterMembers = this.dataPointClusterMembersFunction(dataPoint);

  return this.meanDistance(dataPoint, dataPointClusterMembers);
};

B

SilhouetteCoefficient.prototype.b = function(dataPoint) {
  var dataPointNearestClusterMembers = this.dataPointNearestClusterMembersFunction(
    dataPoint
  );

  return this.meanDistance(dataPoint, dataPointNearestClusterMembers);
};

S

SilhouetteCoefficient.prototype.s = function (a, b) {
  var max = Math.max(a, b);
  if (max === 0) {return 0.0;}

  return (b - a) / max;
};

Multiple data points

To compute the silhouette coefficient for multiple data points we must compute it for each, sum them, and then divide by the number of data points given.

SilhouetteCoefficient.prototype.dataPoints = function (dataPoints, onComplete) {
  var that = this;
  var cycle = function cycle() {
    var score = 0.0;
    if (that.dataPointsIndex === -1) {
      if (that.scores.length === 0) {return score;}
      score = that.scores.reduce(
        function (x, y) {return x + y;}
      ) / that.scores.length;
      that.onComplete(score);
      return score;
    } else {
      that.scores.push(
        that.dataPoint(
          that.dataPoints[that.dataPointsIndex]
        )
      );
      that.dataPointsIndex -= 1;
      window.requestAnimationFrame(cycle);
    }
  };

  if (typeof onComplete === 'undefined') {
      this.onComplete = function (score) {};
  } else {
    this.onComplete = onComplete;
  }
  if (typeof dataPoints === 'undefined') {this.onComplete(0.0);}

  this.dataPoints = dataPoints;
  this.dataPointsIndex = dataPoints.length - 1;
  this.scores = [];

  window.requestAnimationFrame(cycle);
};

The cycle function is the workhorse. It runs with each call to requestAnimationFrame. By using requestAnimationFrame our calls to cycle will queue and thus not lock up the browser window. You will notice that even after k-means finishes, the silhouetteCoefficient takes a bit longer to update but you can still interact with the dots.

Edge cases

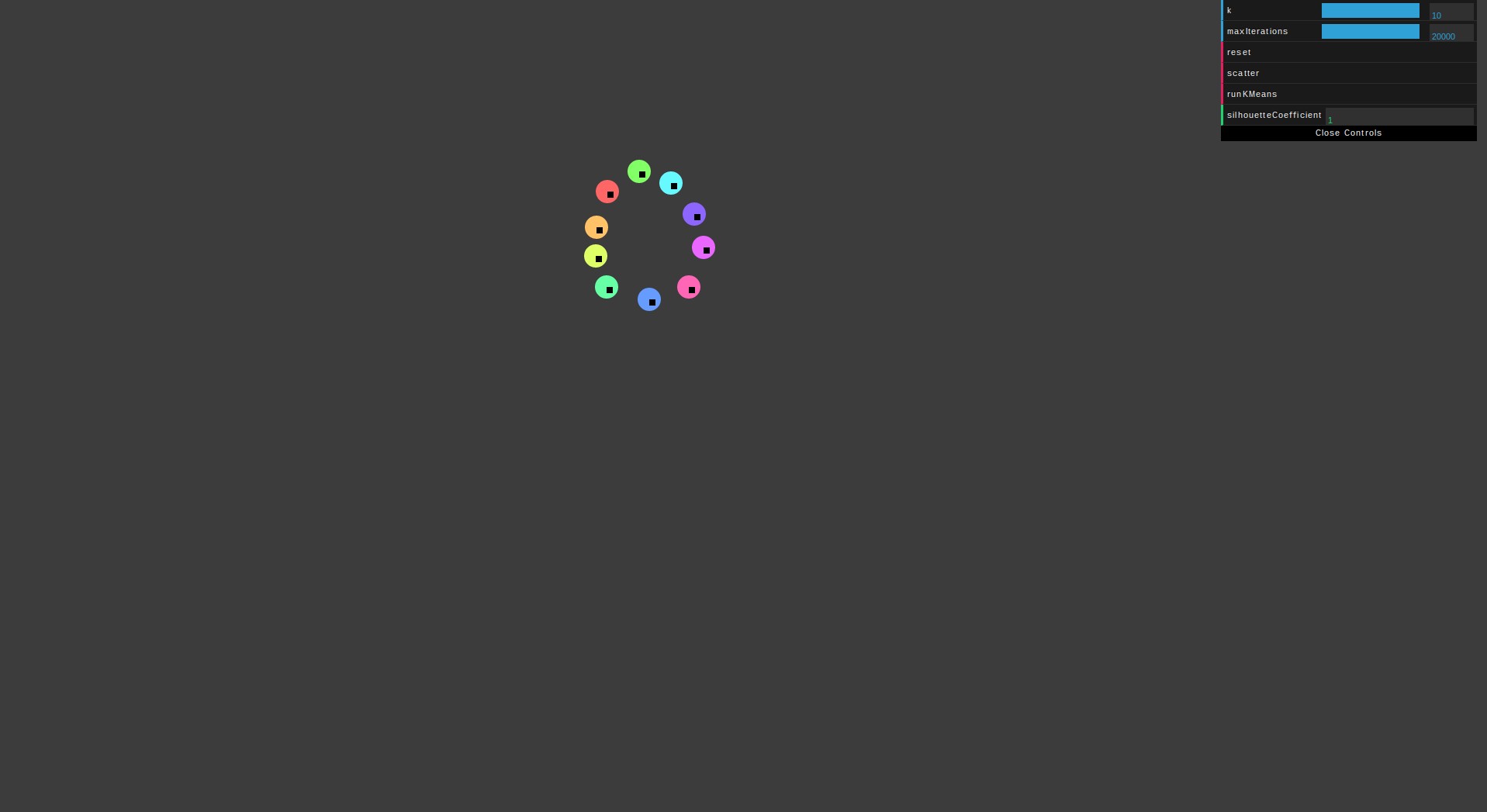
Perfect score when k equals the amount of data points.

An average score of one across all data points indicates that the data is perfectly clustered. As shown above, when k equals the number of data points (10 in this case) you get a perfect silhouette coefficient score. However, this is clearly not 10 clusters but rather just one cluster.

Imperfect score when k is one but the amount of data points is larger.

If we change k to one, you would expect to still receive a perfect score (the circle is clustered nicely) but instead we get the absolute lowest score of -1. When k = 1 but the dataPoints.length > k, the b in s = (b - a)/max(b, a) is zero making s = -1 for each data point. This is because there are no data points in the nearest cluster to the cluster the data point belongs to since that cluster, that the data point belongs to, is the only cluster.

So if you suspect that your data is truly just one cluster and you have more than one sample, the silhouette coefficient is not for you.

Two perfect clusters but the score is not a perfect one.

Clearly we have two perfect clusters and we appropriately set k = 2. However, we only received a score of roughly 0.95 versus the 1 you would have expected. The score was high but not perfect even though our clusters were.

Recap

Using plain vanilla JavaScript, we built the k-means algorithm from scratch as well as the silhouette coefficient metric. We discussed different mean initialization techniques and went into depth about Fouad Kahn’s approach. The assignment and update steps were discussed where the data points are assigned to their closest means and the means are updated by averaging the features of their currently assigned data points. To not lock up our interface we used requestAnimationFrame and cycled our iterations for both k-means and the silhouette coefficient metric. Lastly, we discussed one way of determining how well our data is clustered using the silhouette coefficient metric and went over some unintuitive cases.

Clustering is a viable technique when you have unlabeled data but if you have labeled data take a look at K-Nearest Neighbors from Scratch–a supervised clustering method.

Boost your skills, how to easily write K-Means |