Lettier.com

Let's make a Search Engine with Vue.js |

Overview

Scikit-learn may soon have an implementation of Okapi Best Matching 25 (BM25) given this active pull request. In light of this, we will take a look at how it differs from the more well known term-frequency inverse document-frequency (tf-idf) vector space model (VSM) approach to retrieving relevant information.

In information retrieval, Okapi BM25 (BM stands for Best Matching) is a ranking function used by search engines to rank matching documents according to their relevance to a given search query.

For both tf-idf VSM and BM25, we will build up each technique from scratch. The JavaScript framework, Vue.js, will provide the tools needed to create a two-way data bound interface where each approach can run and rank our input as we type. When we are finished, we will have a search engine capable of retrieving relevant Mother Goose nursery rhymes using both tf-idf VSM and BM25 simultaneously.

Demo

If you would like to play along as we build up the project, there is a playable demo located here.

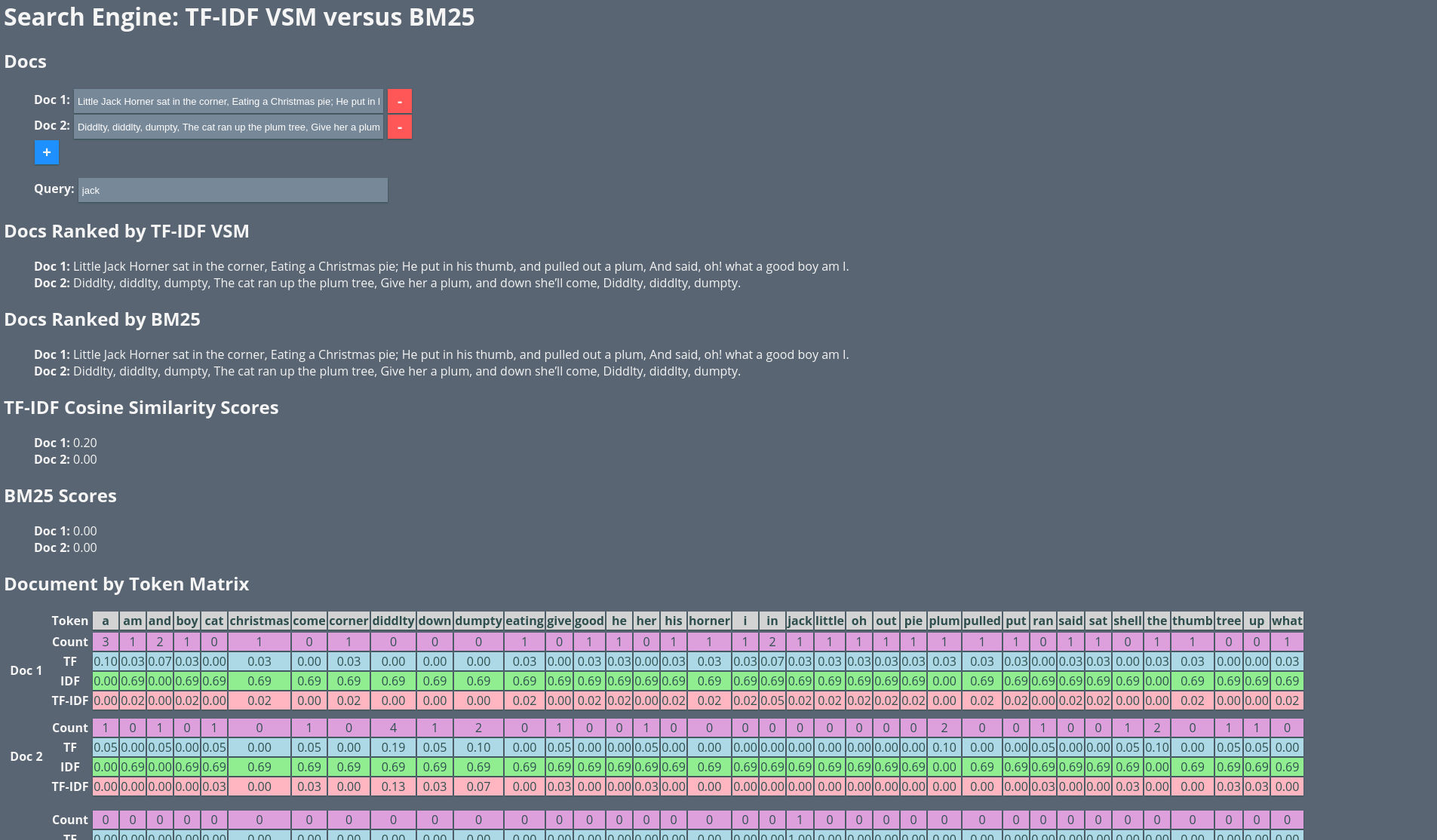
Demo built with Vue.js

Demo built with Vue.js

Preparation

Before we can build the tf-idf VSM and BM25 approaches from scratch, we will need to collect our input documents, scrub them of unwanted characters, tokenize each input document, and assemble our dictionary.

Corpus

Our input documents will come from Project Gutenberg’s Mother Goose or the Old Nursery Rhyme.

In a more real world scenario, one would typically have many more documents but for our purposes this is sufficient.

Scrub

Not all of the characters found in the stream of sequences (the input documents) are needed. We will go ahead and scrub any punctuation character from our documents.

text.toLowerCase().replace(
    /[~`’!@#$%^&*(){}\[\];:"'<,.>?\/\\|_+=-]/g
  , ''
)

Note that we are also lowercasing all characters to avoid any scenario where XyZ and xyZ are considered different during computation. In some cases you may want to keep the letter case when the case adds information. For example, letter case could be a feature during named entity recognition (NER).

Our input documents now look like the following:

Tokenize

At this point we need to shred our documents up into little piles of pieces. This is the bag-of-words model.

In this model, a text (such as a sentence or a document) is represented as the bag (multiset) of its words, disregarding grammar and even word order but keeping multiplicity. 
var makeTokens = function (text) {
  if (text === null) { return []; }
  if (text.length === 0) { return []; }
  return text.toLowerCase().replace(
      /[~`!@#$%^&*(){}\[\];:"'<,.>?\/\\|_+=-’]/g
    , ''
  ).split(' ').filter(function (token) { return token.length > 0; });
};

Our tokens will be one n-grams or unigrams since we are splitting on white space.

["little", "jack", "horner", "sat", "in", "the", "corner", "eating", "a", "christmas", "pie", "he", "put", "in", "his", "thumb", "and", "pulled", "out", "a", "plum", "and", "said", "oh", "what", "a", "good", "boy", "am", "i"]
["diddlty", "diddlty", "dumpty", "the", "cat", "ran", "up", "the", "plum", "tree", "give", "her", "a", "plum", "and", "down", "shell", "come", "diddlty", "diddlty", "dumpty"]
["to", "market", "to", "market", "to", "buy", "a", "plum", "cake", "home", "again", "home", "again", "market", "is", "late", "to", "market", "to", "market", "to", "buy", "a", "plum", "bun", "home", "again", "home", "again", "market", "is", "done"]
["jack", "and", "jill", "went", "up", "the", "hill", "to", "fetch", "a", "pail", "of", "water", "jack", "fell", "down", "and", "broke", "his", "crown", "and", "jill", "came", "tumbling", "after"]

Dictionary

We will now take each shredded pile of tokens and build a dictionary—an array of unique words (unigrams) ordered alphabetically.

, dictionary: function () {
    return this.tokens.reduce(
        function (acc, tokens) {
          return acc.concat(tokens);
        }
      , []
    ).reduce(
        function (acc, word) {
          if (acc.indexOf(word) === -1) {
            acc.push(word);
            return acc;
          } else {
            return acc;
          }
        }
      , []
    ).sort();
  }

TF-IDF VSM

We can now use tf-idf to weight the terms/tokens in each of our bag-of-word documents which will ultimately help rank each document given a query.

Vector Space Model

We could use only tf-idf to rank our documents given a query. One could argue that this would be a more even comparison to BM25. One way to do this would be to do the following (pseudo code).

Q = Query
D = Docs
for every document d in D
  total = 0
  for every query token q in Q
    total += findTfIdfWeight(d, q)
  d.score = total
D = sortDocsByScores(D, descending)

However, we will use the tf-idf weights as the components to our vectorized documents under the vector space model (VSM).

Each dimension corresponds to a separate term. If a term occurs in the document, its value in the vector is non-zero. Several different ways of computing these values, also known as (term) weights, have been developed. One of the best known schemes is tf-idf weighting […].

Ultimately, the document scores—given a query—will be the cosine similarity between the query vector and the document vectors. It is the tf-idf weights, however, that determine where each document ends up in the multidimensional token space.

Count

The term frequency (tf) could simply be the number of times token X occurs in document Y. However, we will be using a different tf variant and so the counts will be a pre-step to computing the term frequencies.

, countVectors: function () {
    return this.tokens.map(
      function (tokens) {
        return this.dictionary.map(
          function (word) {
            return tokens.reduce(
                function (acc, token) { return token === word ? acc + 1 : acc; }
              , 0
            );
          }
        );
      }.bind(this)
    );
  }
, countVectorsT: function () {
    let arr = [];
    this.countVectors.map(
      function (countVector, row, countVectors) {
        countVector.map(
          function (count, col, countVector) {
            if (row === 0) { arr.push([]); }
            arr[col].push(count);
          }
        );
      }
    );
    return arr;
  }

The first function, countVectors, produces a matrix where the rows are the documents, the columns are the tokens, and each cell is the number of observances of token column X in document row Y. The second function, countVectorsT, flips/transposes this around where the rows are the tokens, the columns are the documents, and each cell is the number of observances of token row X in document column Y.

Our document by token/term matrix looks like the following.

Count Matrix

Count Matrix

Term Frequency

For the term frequency we will take the count of the token divided by the sum of the document count vector. For example, say X occurs two times in document Y and Y has four total tokens. In this case, the tf for X for document Y would be 2 / 4 = 0.5.

var makeTfVector = function (countVector) {
  let total = sum(countVector);
  return countVector.map(
    function (count) {
      return total === 0 ? 0 : count / total;
    }
  );
};
// ...
, tfVectors: function () {
    return this.countVectors.map(
      function (countVector) {
        return makeTfVector(countVector);
      }
    );
  }
TF Matrix

TF Matrix

Inverse Document Frequency

For idf, we will be using the

idf(D,t) = log((number of docs D)/(number of docs that have token t))

variant.

So if a token/term is in every document, the idf will be log(X/X) = log(1) = 0.

, idfVectors: function () {
    let total = this.numberOfDocs;
    if (total === 0) { return this.countVectors.map(function () { return []; }); }
    let idfVector = this.countVectors[0].map(
      function (count, col) {
        let inDocCount = this.countVectorsT[col].reduce(
            function (acc, x) {
              return acc + (x > 0 ? 1 : 0);
            }
          , 0
        );
        if (total === 0) { return 0; }
        if (inDocCount === 0) { return 0; }
        return Math.log(total / inDocCount);
      }.bind(this)
    );
    return this.countVectors.map(function () { return idfVector; });
  }

Note that for each document row, its idf row vector is the same for any other document row.

IDF Matrix

IDF Matrix

TF * IDF

Now that we the tf and the idf vectors, we can multiply each component together, per document vector, giving us our final vectorized documents.

, tfIdfVectors: function () {
    return this.tfVectors.map(
      function (tfVector, row) {
        return tfVector.map(
          function (tf, col) {
            return tf * this.idfVectors[row][col];
          }.bind(this)
        );
      }.bind(this)
    );
  }

You will notice that if a token is in all documents, its final tf-idf score is zero (because its idf is zero) for any document in the corpus. When a token is in every document, it is effectively ignored when calculating the relevance of documents in a corpus again a given query. You can see this happening for a in our documents.

When a token’s tf is zero, for a given document vector, its resulting tf-idf score is zero even if its idf is non-zero. This makes sense since the document never had that word or term.

TF-IDF Matrix

TF-IDF Matrix

Query

For the query, we will do the same thing we did to vectorize the corpus documents. We will not alter the idf document vectors based on the query tokens, however. Also, our dictionary will not expand to include any query terms not found in any document.

, queryTokens: function () {
    return makeTokens(this.query);
  }
, queryCountVector: function () {
    return this.dictionary.map(
      function (word) {
        return this.queryTokens.reduce(
            function (acc, token) { return token === word ? acc + 1 : acc; }
          , 0
        );
      }.bind(this)
    );
  }
, queryTfVector: function () {
    return makeTfVector(this.queryCountVector);
  }
, queryIdfVector: function () {
    return this.idfVectors[0];
  }
, queryTfIdfVector: function () {
    return this.queryTfVector.map(
      function (tf, index) {
        return tf * this.queryIdfVector[index];
      }.bind(this)
    );
  }
Query Vectors

Query Vectors

Cosine Similarity

Given our tf-idf query vector and our tf-idf document vectors, we can rank each document’s relevance by calculating the cosine similarity between the query tf-idf vector and each tf-idf document vector.

If the query vector points in the same direction (0 degrees) as a document vector, the cosine similarity will be 1 for an exact or perfect match. However, if a query vector is orthogonal or perpendicular (90 degrees) to a document vector, the cosine similarity with be 0. Finally, if a query vector points in the exact opposite direction (180 degrees) as a document vector, the cosine similarity will be -1.

, cosineSimilarities: function () {
    let mag = function (vector) {
      return Math.sqrt(
        vector.reduce(
            function (acc, el) {
              return acc + (el * el);
            }
          , 0
        )
      );
    };
    let queryMag = mag(this.queryTfIdfVector);
    return this.tfIdfVectors.map(
      function (tfIdfVector) {
        let dot = tfIdfVector.reduce(
            function (acc, tfIdf, index) {
              return acc + (tfIdf * this.queryTfIdfVector[index]);
            }.bind(this)
          , 0
        );
        let docMag = mag(tfIdfVector);
        let mags = queryMag * docMag;
        return mags === 0 ? 0 : dot / mags;
      }.bind(this)
    );
  }

The cosine similarity between a query tf-idf vector and a document tf-idf vector is as follows.

Q = Query
d = Document
cosineSimilarity(Q, d) = dotProduct(Q, d) / (magnitude(Q) * magnitude(d))

Note that the range is [-1, 1].

Ranking

Now that we have the cosine similarity scores, we can finally rank all of the documents in our corpus.

, rankScoredDocs: function (scores) {
    return scores.map(
      function (score, index) {
        let doc = this.docs[index];
        doc.index = index;
        return [score, doc];
      }.bind(this)
    ).sort(function (a, b) { return -a[0] + b[0]; }).map(
      function (elem) {
        return elem[1];
      }
    );
  }
// ...
, tfIdfVsmRankedDocs: function () {
    return this.rankScoredDocs(this.cosineSimilarities);
  }

Okapi BM25

BM25 is not as involved as our tf-idf VSM approach to ranking documents for information retrieval. Our implementation is one large function that reuses the document and query count vectors.

Scoring

We start with finding the average or mean document length by summing up each document count vector and dividing that by the number of documents. With the mean document length in hand, we go through each document count vector and for each one of those, we go through each query token. Given a document count vector and a query token, we calculate the following.

In addition to this, we have the following parameters.

ri is the # of relevant documents containing term i. R is the number of relevant documents for this query. k1 determines how the tf component of the term weight changes as fi increases. k2 has a similar role for the query term weights. K is more complicated. Its role is basically to normalize the tf component by document length. b regulates the impact of length normalization.

The r and R parameters are suspicious. They deal with relevance but the whole reason for using BM25 is to find the relevant documents given a query. We will keep them at zero for the duration of any given query. However, they do allow one to initially set them to zero and then update them with feedback given by the user performing the search query.

The model thus far clearly contains a natural mechanism for relevance feedback — that is, for modifying the query based on relevance information. If we start with no relevance information, then we would weight the terms using the inverse document frequency (IDF) formula. Once the user makes some judgements of relevance, we should clearly reweight the terms according to the RSJ formula.

To gather the BM25 scores, for the documents in our corpus, we need to compute the following.

Pseudo code:

Q = Query
D = Docs
BM25(Q, d) =
  total = 0
  for each query token q in Q
    x     = log(((r+0.5)/(R-r+0.5))/((n-r+0.5)/(N-n-R+r+0.5)))
    y     = ((k1+1)*f)/(K+f)
    z     = ((k2+1)*qf)/(k2+qf)
    total = total+(x*y*z)
  return total
for every document d in D
  d.score = BM25(Q, d)

The actual code:

, bm25Scores: function () {
    let meanDocLen = 0;
    if (this.numberOfDocs > 0) {
      meanDocLen = sum(
        this.countVectors.map(
          function (countVector) {
            return sum(countVector);
          }
        )
      ) / this.numberOfDocs;
    }
    let k1 = 1.2;
    let k2 = 100;
    let b  = 0.75;
    return this.countVectors.map(
      function (countVector) {
        return this.queryTokens.reduce(
            function (acc, queryToken) {
              let dictionaryIndex = this.dictionary.indexOf(queryToken);

              let K  = meanDocLen === 0 ? 0 : k1 * ((1 - b) + (b * (sum(countVector) / meanDocLen)));

              let r  = 0;
              let R  = 0;

              let qf = dictionaryIndex < 0 ? 0 : this.queryCountVector[dictionaryIndex];
              let n  = 0;
              if (dictionaryIndex >= 0) {
                n = this.countVectorsT[dictionaryIndex].reduce(
                    function (acc, x) { return acc + (x > 0 ? 1 : 0); }
                  , 0
                );
              }
              let N = this.numberOfDocs;
              let f = dictionaryIndex < 0 ? 0 : countVector[dictionaryIndex];

              let ai = r + 0.5;
              let bi = R - r + 0.5;
              let ci = n - r + 0.5;
              let di = N - n - R + r + 0.5;
              let ei = bi === 0 ? 0 : ai / bi;
              let fi = di === 0 ? 0 : ci / di;
              let gi = fi === 0 ? 0 : ei / fi;

              let hi = (k1 + 1) * f;
              let ii = K + f;
              let ji = ii === 0 ? 0 : hi / ii;

              let ki = (k2 + 1) * qf;
              let li = k2 + qf;
              let mi = li === 0 ? 0 : ki / li;

              return acc + (Math.log(gi) * ji * mi);
            }.bind(this)
          , 0
        );
      }.bind(this)
    );
  }

Ranking

Similar to what we did with the tf-idf VSM approach, we will rank all of the documents in our corpus. Of course this time the criteria will be their BM25 score.

, rankScoredDocs: function (scores) {
    return scores.map(
      function (score, index) {
        let doc = this.docs[index];
        doc.index = index;
        return [score, doc];
      }.bind(this)
    ).sort(function (a, b) { return -a[0] + b[0]; }).map(
      function (elem) {
        return elem[1];
      }
    );
  }
// ...
, bm25RankedDocs: function () {
    return this.rankScoredDocs(this.bm25Scores);
  }

Comparison

With our approaches in place, we can now use our search engine. Given a query, we will see—simultaneously—how tf-idf VSM and BM25 rank our corpus.

Documents

As stated above, our corpus consists of the following four documents.

Queries

To tease out any differences between the two approaches, we will choose three one word queries that cover the range of cases.

Found in all Documents

The first query will be a. This token is found in all four documents.

Docs Ranked by TF-IDF VSM

Doc 1: Little Jack Horner sat in the corner, Eating a Christmas pie; He put in his thumb, and pulled out a plum, And said, oh! what a good boy am I.
Doc 2: Diddlty, diddlty, dumpty, The cat ran up the plum tree, Give her a plum, and down she’ll come, Diddlty, diddlty, dumpty.
Doc 3: To market, to market, to buy a plum cake, Home again, home again, market is late; To market, to market, to buy a plum bun, Home again, home again, market is done.
Doc 4: Jack and Jill Went up the hill, To fetch a pail of water; Jack fell down And broke his crown, And Jill came tumbling after.

Docs Ranked by BM25

Doc 4: Jack and Jill Went up the hill, To fetch a pail of water; Jack fell down And broke his crown, And Jill came tumbling after.
Doc 2: Diddlty, diddlty, dumpty, The cat ran up the plum tree, Give her a plum, and down she’ll come, Diddlty, diddlty, dumpty.
Doc 3: To market, to market, to buy a plum cake, Home again, home again, market is late; To market, to market, to buy a plum bun, Home again, home again, market is done.
Doc 1: Little Jack Horner sat in the corner, Eating a Christmas pie; He put in his thumb, and pulled out a plum, And said, oh! what a good boy am I.

TF-IDF Cosine Similarity Scores

Doc 1: 0.00
Doc 2: 0.00
Doc 3: 0.00
Doc 4: 0.00

BM25 Scores

Doc 1: -3.37
Doc 2: -2.42
Doc 3: -2.87
Doc 4: -2.27

Since a is present in all documents its idf is zero. Thus its tf-idf is zero and tf-idf VSM essentially ignores the query and returns the documents in the same order as they were inputted.

The BM25 order is four, two, three, and one. Document four repeats a one time as does document two. Document one and three repeat a three and two times respectively. If you count them up, document two is slightly smaller in length than document four. Document one and three are both longer than document two and four.

Doc 3 length: 32
Doc 1 length: 30
Doc 4 length: 25
Doc 2 length: 21

Found in one Document

The second query will be hill which is only found in one document—document four.

Docs Ranked by TF-IDF VSM

Doc 4: Jack and Jill Went up the hill, To fetch a pail of water; Jack fell down And broke his crown, And Jill came tumbling after.
Doc 1: Little Jack Horner sat in the corner, Eating a Christmas pie; He put in his thumb, and pulled out a plum, And said, oh! what a good boy am I.
Doc 2: Diddlty, diddlty, dumpty, The cat ran up the plum tree, Give her a plum, and down she’ll come, Diddlty, diddlty, dumpty.
Doc 3: To market, to market, to buy a plum cake, Home again, home again, market is late; To market, to market, to buy a plum bun, Home again, home again, market is done.

Docs Ranked by BM25

Doc 4: Jack and Jill Went up the hill, To fetch a pail of water; Jack fell down And broke his crown, And Jill came tumbling after.
Doc 1: Little Jack Horner sat in the corner, Eating a Christmas pie; He put in his thumb, and pulled out a plum, And said, oh! what a good boy am I.
Doc 2: Diddlty, diddlty, dumpty, The cat ran up the plum tree, Give her a plum, and down she’ll come, Diddlty, diddlty, dumpty.
Doc 3: To market, to market, to buy a plum cake, Home again, home again, market is late; To market, to market, to buy a plum bun, Home again, home again, market is done.

TF-IDF Cosine Similarity Scores

Doc 1: 0.00
Doc 2: 0.00
Doc 3: 0.00
Doc 4: 0.23

BM25 Scores

Doc 1: 0.00
Doc 2: 0.00
Doc 3: 0.00
Doc 4: 0.87

In this case, both tf-idf VSM and BM25 ranked the corpus the same. You will notice that document four is indeed the most relevant with all others having the same score no matter the approach.

Found in some Documents

Our final query will be and. Much like a, and is usually considered a stop word and is filtered out during preprocessing. Since we did not filter out and, the token is present in three documents.

Docs Ranked by TF-IDF VSM

Doc 4: Jack and Jill Went up the hill, To fetch a pail of water; Jack fell down And broke his crown, And Jill came tumbling after.
Doc 1: Little Jack Horner sat in the corner, Eating a Christmas pie; He put in his thumb, and pulled out a plum, And said, oh! what a good boy am I.
Doc 2: Diddlty, diddlty, dumpty, The cat ran up the plum tree, Give her a plum, and down she’ll come, Diddlty, diddlty, dumpty.
Doc 3: To market, to market, to buy a plum cake, Home again, home again, market is late; To market, to market, to buy a plum bun, Home again, home again, market is done.

Docs Ranked by BM25

Doc 3: To market, to market, to buy a plum cake, Home again, home again, market is late; To market, to market, to buy a plum bun, Home again, home again, market is done.
Doc 2: Diddlty, diddlty, dumpty, The cat ran up the plum tree, Give her a plum, and down she’ll come, Diddlty, diddlty, dumpty.
Doc 1: Little Jack Horner sat in the corner, Eating a Christmas pie; He put in his thumb, and pulled out a plum, And said, oh! what a good boy am I.
Doc 4: Jack and Jill Went up the hill, To fetch a pail of water; Jack fell down And broke his crown, And Jill came tumbling after.

TF-IDF Cosine Similarity Scores

Doc 1: 0.09
Doc 2: 0.04
Doc 3: 0.00
Doc 4: 0.15

BM25 Scores

Doc 1: -1.13
Doc 2: -0.93
Doc 3: 0.00
Doc 4: -1.35

As stated above, and does not appear in every document. Unlike a, it was not filtered out by tf-idf VSM since it did not have a zero idf. The tf-idf VSM ranking makes sense since document four, one, two, and three repeated and three, two, one, and zero times respectively.

Looking at the BM25 ranking, you would think there was a bug in the source code. BM25 ranked the corpus in the reverse order—from the document with the least amount of ands to the document with most amount of ands. Document three was zero since

y = ((k1+1)*f)/(K+f)

(found in the pseudo code) was zero. Recall that f is the amount of times the query token is found in the document being evaluated. In this case, f equals how many times and appears in document three.

For the remaining documents, the idf portion

x = log(((r+0.5)/(R-r+0.5))/((n-r+0.5)/(N-n-R+r+0.5)))

of the equation was negative since the input into the log function was less than one. For our version of BM25, we have a problem when one of the query terms are found in more than half of the documents in our corpus. Note that adding more ands in the query does not change the BM25 ranking.

Recap

Using Vue.js, we built a JavaScript based search engine that uses both tf-idf VSM and Okapi BM25. For every given query, our search engine ran both approaches in tandem, allowing us to explore the similarities and differences between each document ranking method.

Appendix

Below you will find some supplementary material.

Full Source Code

Listed below are all of the source code files needed to build the project described up above.

index.js

/*
  David Lettier (C) 2016
  http://www.lettier.com/
*/

// jshint esversion: 6
// jshint laxbreak:  true
// jshint laxcomma:  true

var sum = function (arr) {
  return arr.reduce(function (acc, x) { return acc + x; }, 0);
};
var makeTokens = function (text) {
  if (text === null) { return []; }
  if (text.length === 0) { return []; }
  return text.toLowerCase().replace(
      /[~`’!@#$%^&*(){}\[\];:"'<,.>?\/\\|_+=-]/g
    , ''
  ).split(' ').filter(function (token) { return token.length > 0; });
};
var makeTfVector = function (countVector) {
  let total = sum(countVector);
  return countVector.map(
    function (count) {
      return total === 0 ? 0 : count / total;
    }
  );
};
var app = new Vue({
    el: "#app"
  , data: {
        docs: [
        ]
      , query: null
    }
  , methods: {
        addDoc: function () {
          this.docs.push({text: "", id: Date.now()});
          this.$nextTick(
            this.docsNavSetup
          );
        }
      ,  removeDoc: function (button) {
          let id = parseInt(button.target.attributes.docId.value, 10);
          this.docs = this.docs.filter(
            function (doc) {
              return (doc.id !== id);
            }
          );
        }
      , rankScoredDocs: function (scores) {
          return scores.map(
            function (score, index) {
              let doc = this.docs[index];
              doc.index = index;
              return [score, doc];
            }.bind(this)
          ).sort(function (a, b) { return -a[0] + b[0]; }).map(
            function (elem) {
              return elem[1];
            }
          );
        }
      , docsNavSetup: function () {
          this.docs.map(
            function (doc, index, docs) {
              let el = document.getElementById(doc.id.toString());
              if (el === null) { return; }
              el.tabIndex = (index + 1).toString();
              if (index === (docs.length - 1)) {
                el.focus();
              } else {
                el.blur();
              }
            }
          );
        }
    }
  , computed: {
        parsedDocs: function () {
          return this.docs.map(
            function (doc) {
              return {
                  tokens: makeTokens(doc.text)
                , id: doc.id
              };
            }
          );
        }
      , tokens: function () {
          return this.parsedDocs.map(
              function (parsedDoc) { return parsedDoc.tokens || []; }
          );
        }
      , dictionary: function () {
          return this.tokens.reduce(
              function (acc, tokens) {
                return acc.concat(tokens);
              }
            , []
          ).reduce(
              function (acc, word) {
                if (acc.indexOf(word) === -1) {
                  acc.push(word);
                  return acc;
                } else {
                  return acc;
                }
              }
            , []
          ).sort();
        }
      , numberOfDocs: function () {
          return this.countVectors.reduce(
              function (acc, x, index) {
                return acc + (this.countVectors[index].length === 0 ? 0 : 1);
              }.bind(this)
            , 0
          );
        }
      , countVectors: function () {
          return this.tokens.map(
            function (tokens) {
              return this.dictionary.map(
                function (word) {
                  return tokens.reduce(
                      function (acc, token) { return token === word ? acc + 1 : acc; }
                    , 0
                  );
                }
              );
            }.bind(this)
          );
        }
      , countVectorsT: function () {
          let arr = [];
          this.countVectors.map(
            function (countVector, row, countVectors) {
              countVector.map(
                function (count, col, countVector) {
                  if (row === 0) { arr.push([]); }
                  arr[col].push(count);
                }
              );
            }
          );
          return arr;
        }
      , tfVectors: function () {
          return this.countVectors.map(
            function (countVector) {
              return makeTfVector(countVector);
            }
          );
        }
      , idfVectors: function () {
          let total = this.numberOfDocs;
          if (total === 0) { return this.countVectors.map(function () { return []; }); }
          let idfVector = this.countVectors[0].map(
            function (count, col) {
              let inDocCount = this.countVectorsT[col].reduce(
                  function (acc, x) {
                    return acc + (x > 0 ? 1 : 0);
                  }
                , 0
              );
              if (total === 0) { return 0; }
              if (inDocCount === 0) { return 0; }
              return Math.log(total / inDocCount);
            }.bind(this)
          );
          return this.countVectors.map(function () { return idfVector; });
        }
      , tfIdfVectors: function () {
          return this.tfVectors.map(
            function (tfVector, row) {
              return tfVector.map(
                function (tf, col) {
                  return tf * this.idfVectors[row][col];
                }.bind(this)
              );
            }.bind(this)
          );
        }
      , docsVectors: function () {
          return this.countVectors.map(
            function (countVector, index) {
              return [countVector, this.tfVectors[index], this.idfVectors[index], this.tfIdfVectors[index]];
            }.bind(this)
          );
        }
      , queryTokens: function () {
          return makeTokens(this.query);
        }
      , queryCountVector: function () {
          return this.dictionary.map(
            function (word) {
              return this.queryTokens.reduce(
                  function (acc, token) { return token === word ? acc + 1 : acc; }
                , 0
              );
            }.bind(this)
          );
        }
      , queryTfVector: function () {
          return makeTfVector(this.queryCountVector);
        }
      , queryIdfVector: function () {
          return this.idfVectors[0];
        }
      , queryTfIdfVector: function () {
          return this.queryTfVector.map(
            function (tf, index) {
              return tf * this.queryIdfVector[index];
            }.bind(this)
          );
        }
      , cosineSimilarities: function () {
          let mag = function (vector) {
            return Math.sqrt(
              vector.reduce(
                  function (acc, el) {
                    return acc + (el * el);
                  }
                , 0
              )
            );
          };
          let queryMag = mag(this.queryTfIdfVector);
          return this.tfIdfVectors.map(
            function (tfIdfVector) {
              let dot = tfIdfVector.reduce(
                  function (acc, tfIdf, index) {
                    return acc + (tfIdf * this.queryTfIdfVector[index]);
                  }.bind(this)
                , 0
              );
              let docMag = mag(tfIdfVector);
              let mags = queryMag * docMag;
              return mags === 0 ? 0 : dot / mags;
            }.bind(this)
          );
        }
      , bm25Scores: function () {
          let meanDocLen = 0;
          if (this.numberOfDocs > 0) {
            meanDocLen = sum(
              this.countVectors.map(
                function (countVector) {
                  return sum(countVector);
                }
              )
            ) / this.numberOfDocs;
          }
          let k1 = 1.2;
          let k2 = 100;
          let b  = 0.75;
          return this.countVectors.map(
            function (countVector) {
              return this.queryTokens.reduce(
                  function (acc, queryToken) {
                    let dictionaryIndex = this.dictionary.indexOf(queryToken);

                    let K  = meanDocLen === 0 ? 0 : k1 * ((1 - b) + (b * (sum(countVector) / meanDocLen)));

                    let r  = 0;
                    let R  = 0;

                    let qf = dictionaryIndex < 0 ? 0 : this.queryCountVector[dictionaryIndex];
                    let n  = 0;
                    if (dictionaryIndex >= 0) {
                      n = this.countVectorsT[dictionaryIndex].reduce(
                          function (acc, x) { return acc + (x > 0 ? 1 : 0); }
                        , 0
                      );
                    }
                    let N = this.numberOfDocs;
                    let f = dictionaryIndex < 0 ? 0 : countVector[dictionaryIndex];

                    let ai = r + 0.5;
                    let bi = R - r + 0.5;
                    let ci = n - r + 0.5;
                    let di = N - n - R + r + 0.5;
                    let ei = bi === 0 ? 0 : ai / bi;
                    let fi = di === 0 ? 0 : ci / di;
                    let gi = fi === 0 ? 0 : ei / fi;

                    let hi = (k1 + 1) * f;
                    let ii = K + f;
                    let ji = ii === 0 ? 0 : hi / ii;

                    let ki = (k2 + 1) * qf;
                    let li = k2 + qf;
                    let mi = li === 0 ? 0 : ki / li;

                    return acc + (Math.log(gi) * ji * mi);
                  }.bind(this)
                , 0
              );
            }.bind(this)
          );
        }
      , tfIdfVsmRankedDocs: function () {
          return this.rankScoredDocs(this.cosineSimilarities);
        }
      , bm25RankedDocs: function () {
          return this.rankScoredDocs(this.bm25Scores);
        }
    }
});

index.html

<!DOCTYPE HTML>
<!--
  David Lettier (C) 2016.
  http://www.lettier.com
-->
<html lang="en">
  <head>
    <meta charset="UTF-8">
    <meta name="description" content="JavaScript search engine that compares TF-IDF VSM and BM25.">
    <meta name="keywords" content="javascript,tf,idf,bm25,okapi,lettier,david">
    <meta name="author" content="David Lettier">
    <title>Search Engine: TF-IDF VSM versus BM25 | Lettier.com</title>
    <link rel="stylesheet" type="text/css" href="index.css">
  </head>
  <body>
    <div id="app">
      <h1>Search Engine: TF-IDF VSM versus BM25</h1>
      <h2>Docs</h2>
      <ul>
        <li v-for="(doc, index) in docs">
          <b>Doc {{index + 1}}:</b> <input placeholder="Input a document." v-bind:id="doc.id" v-model="doc.text">
          <button class="removeDocButton" v-on:click="removeDoc" v-bind:docId="doc.id" title="Remove Doc">-</button>
        </li>
        <button class="addDocButton" v-on:click="addDoc" title="Add Doc">+</button>
      </ul>
      <ul>
        <li><b>Query:</b> <input placeholder="Input a query." v-model="query"></li>
      </ul>
      <template v-if="docs.length">
        <template v-if="queryTokens.length">
          <template v-if="tfIdfVsmRankedDocs.length">
            <h2>Docs Ranked by TF-IDF VSM</h2>
            <ul>
              <template v-for="tfIdfRankedDoc in tfIdfVsmRankedDocs">
                <li><b>Doc {{tfIdfRankedDoc.index + 1}}:</b> {{tfIdfRankedDoc.text}}</li>
              </template>
            </ul>
          </template>
          <template v-if="bm25RankedDocs.length">
            <h2>Docs Ranked by BM25</h2>
            <ul>
              <template v-for="bm25RankedDoc in bm25RankedDocs">
                <li><b>Doc {{bm25RankedDoc.index + 1}}:</b> {{bm25RankedDoc.text}}</li>
              </template>
            </ul>
          </template>
          <template v-if="cosineSimilarities.length">
            <h2>TF-IDF Cosine Similarity Scores</h2>
            <ul>
              <template v-for="(cosineSimilarity, index) in cosineSimilarities">
                <li><b>Doc {{index + 1}}:</b> {{cosineSimilarity.toFixed(2)}}</li>
              </template>
            </ol>
          </template>
          <template v-if="bm25Scores.length">
            <h2>BM25 Scores</h2>
            <ul>
              <template v-for="(bm25Score, index) in bm25Scores">
                <li><b>Doc {{index + 1}}:</b> {{bm25Score.toFixed(2)}}</li>
              </template>
            </ul>
          </template>
        </template>
        <template v-if="docsVectors.length && dictionary.length">
          <h2>Document by Token Matrix</h2>
          <div class="matrixContainer">
            <table>
              <tr>
                <td></td>
                <td>
                  <b>Token</b>
                </td>
                <template v-for="word in dictionary">
                  <th class="token">{{word}}</th>
                </template>
              </tr>
              <template v-for="(docVector, index) in docsVectors">
                <tr>
                  <td rowspan="5">
                    <b>Doc {{index + 1}}</b>
                  </td>
                </tr>
                <tr>
                  <td><b>Count</b></td>
                  <template v-for="count in docVector[0]">
                    <td class="count">{{count}}</td>
                  </template>
                </tr>
                <tr>
                  <td><b>TF</b></td>
                  <template v-for="tf in docVector[1]">
                    <td class="tf">{{tf.toFixed(2)}}</td>
                  </template>
                </tr>
                <tr>
                  <td>
                    <b>IDF</b>
                  </td>
                  <template v-for="idf in docVector[2]">
                    <td class="idf">{{idf.toFixed(2)}}</td>
                  </template>
                </tr>
                <tr>
                  <td>
                    <b>TF-IDF</b>
                  </td>
                  <template v-for="tfIdf in docVector[3]">
                    <td class="tfIdf">{{tfIdf.toFixed(2)}}</td>
                  </template>
                </tr>
                <tr>
                  <template v-for="tfIdf in docVector[3]">
                    <td></td>
                  </template>
                </tr>
                <tr>
                  <template v-for="tfIdf in docVector[3]">
                    <td></td>
                  </template>
                </tr>
              </template>
              <template v-if="queryTokens">
                <tr>
                  <td rowspan="7">
                    <b>Query</b>&nbsp;
                  </td>
                </tr>
                <tr>
                  <template v-for="count in queryCountVector">
                    <td></td>
                  </template>
                </tr>
                <tr>
                  <template v-for="count in queryCountVector">
                    <td></td>
                  </template>
                </tr>
                <tr>
                  <td><b>Count</b></td>
                  <template v-for="count in queryCountVector">
                    <td class="count">{{count}}</td>
                  </template>
                </tr>
                <tr>
                  <td><b>TF</b></td>
                  <template v-for="tf in queryTfVector">
                    <td class="tf">{{tf.toFixed(2)}}</td>
                  </template>
                </tr>
                <tr>
                  <td><b>IDF</b></td>
                  <template v-for="idf in queryIdfVector">
                    <td class="idf">{{idf.toFixed(2)}}</td>
                  </template>
                </tr>
                <tr>
                  <td><b>TF-IDF</b>&nbsp;</td>
                  <template v-for="tfIdf in queryTfIdfVector">
                    <td class="tfIdf">{{tfIdf.toFixed(2)}}</td>
                  </template>
                </tr>
              </template>
            </table>
          </div>
          <div class="matrixContainerSpacer">&nbsp;</div>
        </template>
      </template>
      <div id="logoContainer">
        <a href="#" onclick="window.open('http://www.lettier.com/')" title="Lettier">
          <img id="logo" src="logo.png" width="250" height="250" alt="Lettier">
        </a>
      </div>
    </div>
    <script src="vue.js"></script>
    <script src="index.js"></script>
  </body>
</html>

index.css

/*
  David Lettier (C) 2016.
  http://www.lettier.com/
*/
html {
  height: 100%;
  width: 100%;
}
body {
  font-family: 'Open Sans', Helvetica, Arial, sans-serif;
  background-color: #596572;
  color: whitesmoke;
  height: 100%;
  margin: 0px;
  margin-left: 5px;
  margin-right: 5px;
  padding: 0px;
}
h1 {
  margin-top: 0px;
}
table {
  white-space: nowrap;
}
li {
  list-style: none;
}
th, td {
  text-align: center;
}
input {
  width: 400px;
  height: 30px;
  margin: 1px;
  padding-left: 5px;
  padding-right: 5px;
  background-color: lightslategrey;
  border: none;
  outline: none;
  box-shadow: 0px 1px 1px darkslategrey;
  color: white;
}
button {
  border: none;
  font-size: 20px;
  font-weight: bold;
  width:  32px;
  height: 32px;
  margin: 1px;
  outline: none;
  box-shadow: 0px 1px 1px darkslategrey;
  vertical-align: bottom;
}
.addDocButton {
  background-color: dodgerblue;
  color: whitesmoke;
}
.removeDocButton {
  background-color: #ff5757;
  color: whitesmoke;
}
.token {
  background-color: lightgrey;
  box-shadow: 0px 1px 1px darkslategrey;
  color: darkslategrey;
}
.count {
  background-color: plum;
  box-shadow: 0px 1px 1px darkslategrey;
  color: darkslategrey;
}
.tf {
  background-color: lightblue;
  box-shadow: 0px 1px 1px darkslategrey;
  color: darkslategrey;
}
.idf {
  background-color: lightgreen;
  box-shadow: 0px 1px 1px darkslategrey;
  color: darkslategrey;
}
.tfIdf {
  background-color: lightpink;
  box-shadow: 0px 1px 1px darkslategrey;
  color: darkslategrey;
}
.matrixContainer {
  overflow: auto;
  width: 100%;
}
.matrixContainerSpacer {
  padding-bottom: 100px;
}
#app {
  position: relative;
  min-height: 100%;
}
#logoContainer {
  width: 100%;
  text-align: right;
  position: absolute;
  bottom: 0px;
  padding-right: 5px;
}
#logo {
  width: 100px;
  height: 100px;
}
::-webkit-input-placeholder {
  color: #c6e2ff;
}
::-moz-placeholder {
  color: #c6e2ff;
}
:-ms-input-placeholder {
  color: #c6e2ff;
}
:-moz-placeholder {
  color: #c6e2ff;
}

Hi there! Browse and subscribe to the RSS feed for more content.

2017 David Lettier